Friendship Bracelets: Deconstructing the Triangle Wave

A Seminar at UCSB

Deconstructing the Triangle Wave

Abstract

The speaker's analog circuits explore novel uses of simple components to yield chaotic and rich electronic timbres. Using examples such as "deconstructing the triangle wave," he will explain porting these concepts to a new, digital synthesizer, the Shnth. Ensuing topics include carving a squishable case, and classic computer music in embedded systems.

Biography

Peter Blasser, designer and builder of synthesizers at ciat-lonbarde.net, practices deep consultation with clients who seek rich interactions with their electronics. The instruments manifest electronic modulations through nodes, case flexure, and radio fields. He teaches circuit design and instrument building in classes and workshops, culminating in performance or installation. Some paper circuits can be downloaded from his website, printed out, and assembled to yield sound objects. The cybernetic interface uses the subtleties of touch, through discrete components, often "woven" together geometrically, to simulate intuitive patterns and chaotic sophistication. His designs are spurred into existence to explore platonic or philosophical concepts, which then acquire a narrative as they are refined into essential analog synthesizers.

Analog Synthesis of Triangle Waves

I would first like to demonstrate an analog synthesizer, the Sidrax Organ.  Seven flexible wooden bars sense performative squish, sonifying it through seven essential triangle oscillators.  It is an amplitude modulation; the instrument is silent when un-touched, and electronic tone loudens with pressure.  There are forty-two nodes that when patched by wire or touch, connect voltage representation of said squish and the triangle waves to frequency modulation and glitch inputs, to be detailed.  The synthesynthesist learns to make a triangle oscillator very early on, however, it is durable through a wide range of modifications and enhancements.  Furthermore, it can be used as sub-component for more sophisticated assemblages.  

saw variations and clean triangle

The triangle wave is a sort of mechanical system that, in analog electronics, features one capacitor that charges and discharges in alternate strokes, controlled by a hysteresis mechanism that sets its bounds.  The speed at which it bounces is the usual method of modulation, and this bounce can be further split into two branches- the speed going up and that going down.  This is the source of the saw wave and various other articulations between it and the essential triangle wave, which has equal speeds up and down.

The first point I would like to make is that there are actually two ways of modulating a triangle wave- controlling its bounce as already mentioned, and also controlling its bounds.  Actually bounds modulation is practiced quite often, but not distinguished from the other way; hobbyists with the old and brutal "555" chip, when modulating, are actually controlling the top breakpoint,"threshold" of a saw-triangle amalgam. This method is shunned by the more sophisticated synthesynthesists, because it only modulates the bounds,which is an instant in time rather than the continuous modulation of bounce.  Bounds modulation is also the route to sync-lock circuits; when the modulator is faster than the carrier, it generates an integer-locked undertone series.  This is the magic key to what we will talk about later in the digital emulation of these circuits.  But for now, we have opened triangle wave oscillators to two kinds of modulation, bounds and bounce.  The two taken together offer rich ways to control the wave:

modulating bounce and bounds

A hi-fi enthusiast's reaction to the triangle wave is anxiety about infinite energy present in its sharp peaks.  This energy is theorized by fourier analysis of the "perfect" wave, concluding that a harmonic series extending to infinity is the source of the transients.  These frequencies, and thus energies, will break speaker cones of the hi-fi set.  Of course, in reality they are rolled off, but it is an interesting reaction due to the fourier-dependency of acoustic theory. 

A triangle rotated becomes square steps on a staircase; the triangle and square wave go hand in hand, for the square signal is involved in the mechanism of the hysteresis loop, which decides instantaneously to reflect the wave in opposite direction, or sign change.

When a boy sees a triangle wave, he will most likely see shark teeth; a geologist, freshly formed tectonic mountains without rounding erosion.  I like to see the tail ridges of a basilisk or iguana.

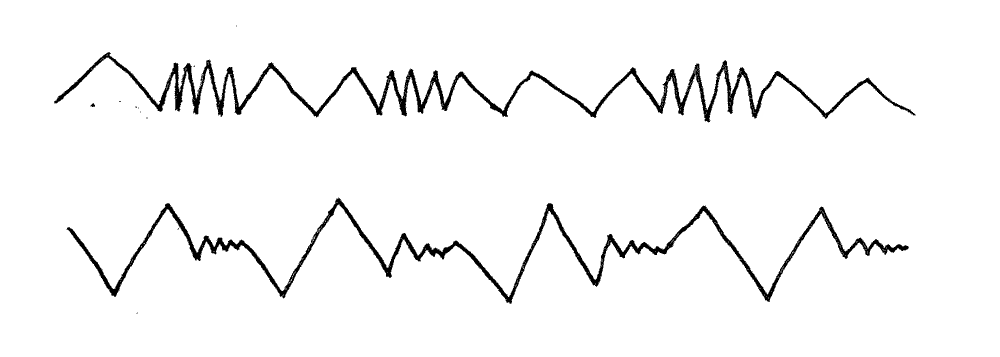bounce is the slope or speed, bounds changes the height or depth

Listen to mylar chips-bags crackling nearby as someone eats a sandwich.  As a misophonist, I am repulsed by and attracted to these crackling and crinkling sounds made from impulses of mylar folds flipping from concave to convex.  They are an explosion across the spectrum made from sharp changes; mylar is the only plastic that generates ultrasound, and one can easily distinguish it clearly from all the other synthesized sounds in our environment.  Listen to it, especially with high pressure in one's ears, and note the difficulty of reproducing these crinkles by fourier methods; it is hard to mp3 compress a chips-bag.  I am spurred by ASMR studies to bring these sounds about for the benefit of listeners who hate sounds, so that they may love them again.  Two ways to do this:

1. physically construct sculptural mechanisms such as coke bubbles in aluminum or solenoids that squish candy wrappers.  Note that misophonists often need a conscious target for their sound-rage, and if the same sounds are generated by a machine, the anger is diffused.
2. electronically synthesize the chips-bag.  here is where assemblage of triangles comes to the fore.

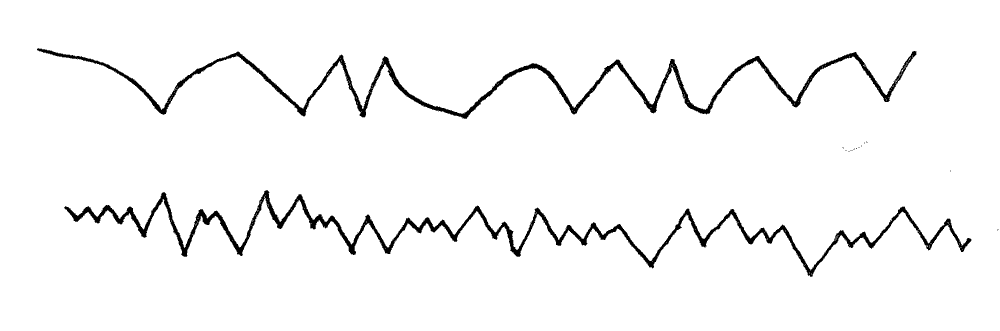bounce and bounds modulation discloses chaos

Triangle Wave Assemblage

Now I'd like to describe a few circuits that combine triangle waves to break out the inherent possibilities of sharp peaks and modulation to make chaos, or the afore-mentioned "chips-bag".  Fourses was originally a kit to make "novel musical sounds," available from Ciat-Lonbarde.  It was inspired by the thinking detailed above, about modulating both bounce and bounds, to see what happens when oscillators bounce off of each other.  Four horses is the metaphor of the naming, but it may be easier to think of them as bouncy balls in a greased tube of their diameter plus a little breathing room so they can move smoothly but not pass each other.  Incidentally, this is the same sort of thought experiment used in particle studies to highlight how particles of the same sort are indistinguishable from each other so they may be thought of as bouncing or passing through each other.  However, these particles are distinguishable, for they have separate bounce controls for each one; traditional fm modulation of slope makes them unique operators in the experiment.  When they bounce, then, they create triangular waves of chaos in the system, to be sampled and enjoyed by all via electro-acoustic diffusion.  

fourses mentality: bouncing off of each other's contingent bounds

I am bringing Fourses back in the near future, and I would like to demonstrate how these circuits are initially prototyped on paper.  On paper circuit, that is.  I have constructed the four oscillators, and their analog switches connecting bounds to each other, with four knobs in the middle to explore the various settings of bounce that make the assemblage more or less reactive.  This instrument is also nodal, in that it has many touch points, for circuit-bending the apparatus and creating further modalities.

Nodal synthesis is not the topic of this discussion, but it is fruitful in triangle waves, because their synthesizer is a mechanism that you can "go into" to massage its inner, soft workings.  The charge capacitor and hysteresis loop are circuit bending points that correspond to the formal modulations of bounce and bounds respectively.   Another instrument that uses nodes as well as the formal modulations is the sidrax organ.  In this organ, which I demonstrated earlier, I wanted to take the modalities of fourses, generalize them, and offer gestural control via the wooden bars.  The seven oscillators are arranged in a circle, for continuous bounce modulation from one to the other, controlled by an aptly named "chaos knob".  In addition, each oscillator has two nodes, called "glitch" inputs, which rewire their bounds to refer to other oscillators, as in the fourses.  The difference is, that sidrax has a "ground state" where each triangle operates within fixed, normalized bounces, yielding a perfect, singular frequency wave.  I've found it important to have such a base state to start performance, and take it from there.

schematic of sidrax organ

Tricentric Logics for Analog Synths

Recently, I've been doing some theoretical work, stemming from the writings of Anthony Braxton.  I am inspired by his use of the word "logics," in the plural, to suggest that a multiplicity can exist in logical schemata; this notion seems to overlap somewhat with the assemblage theory of Manual de Landa, derived from the concepts of, of course, Mrz. Deleuze+Guattari and their Mille Plateaux.  In his new materialism, de Landa outlines how assemblages are generated by materials, and that there is something of a universal singularity, or over-arching diagrams that can be shared amongst assemblages.  In contrast, the unique assemblage is its own individual singularity.  That is, synths have diagrams that may disclose universalisms, while having idiosyncrasies in their resistors, transistors, and capacitors, not to mention wiring, knobbage, and modulation decisions, that make them unique.  One schematic propogated by Braxton is tricentric logics, or an overlay of musical groupings based on three symbols: the circle, triangle, and square.  I am working, in describing the Plumbutter synthesizer, to use tricentric logics to describe the immanent diagrams of analog synths, to describe the underlying mythologies of the synth chain.  For example, rounded versus sharp is the dialectic of most analog sounds; vco is the angular part, and vcf is the resonator of sinus frequencies.  

resonant excitation, or spiral if viewed in polar imaginary

If we take this point about round versus sharp, we have almost finished porting tricentric logics to analog synths.  You see, the round is the circle symbol, which literally happens if you run a resonant filter at saturation; a sine wave is one axis of a circle.  The other, angular part, all our triangle and saw waves, is the triangle symbol.  The only symbol left is the square, but we know that square waves are important in synths too; they are the pseudo-digital logics provided by 4000 series chips, as well as all the multi-stable, primitive transistor circuits. 

All this symbolization is fine and dandy, but where does it get us?  One benefit of porting diagrams, is to think and ask questions such as, if a circle resonator has an "input", as a filter, what would it mean if a triangle had an input?  Can we make a triangle wave behave like a spiral?  This question became of interest when designing a game, Mikey Walker, which we shall get to.  Basically, I needed more ways for the enemies to act when punched.  They were all resonating, and I wanted some to resonate in a triangular way.  Thus the "zwave" came about.  It is like a resonance in that it has an input, but it dissipates this energy by wavering with sharp rather than rounded peaks, and because this is a sort of bounds modulation, you can see that it gets faster as the wave dies out:

zwave has input, gets faster due to bounds shrinkage

The name, "zwave" came from classification work I was doing of curves, looking at sensor data.  When you flex a bar, it makes a sort of "scurve", a rounded form that first goes above zero, and then below.  There came a need, in designing the shnth, to make a facsimile of this, called the zcurve, which is one segment, or a "one-shot," of a triangle wave, which is triggered by external event.  We shall see that this is part of the process of enabling a primitive sort of granular synthesis in its matrix.

curves generated by organic sensor such as piezo, and triangular facsimile

Now you may be confused by the use of a one-shot that has two peaks, one above and one below zero.  It is actually a unique sound to have grains made from these events; it corresponds to the daoist and pretty much everyone else's need for complimentarity, "yin and yang", or from the arp 2000 users' manual "to and fro".  However, the Shnth has two synthesis modes, Dirac and Arab, which offer signed and unsigned maths, respectively.  Those curves are in Dirac mode, because they go positive and negative.  But if you look at them in Arab mode, you see they strongly resemble grain envelopes:

those same curves in arab mode, with no negative numbers

This was the process of enabling a very primitive, embedded granular synthesis in the Shnth: make triangle waves, then make one-shot, triggerable "swoops" to envelope them.  Let's move on to a few comments about digital, then I would like to demonstrate the applications that work with the Shnth.

Interlude: Shnth Description

The Shnth, by Shbobo, is a computer music device that features the ARM Cortex M3 32 bit processor. It connects to host computer via USB, wherein the host computer (windows, linux, or macintosh) may read its "squish data" and create graphics and sound. Or, the Shnth itself is a standalone synthesizer, which may be programmed by host in the new language, "Shlisp", by Shbobo. It is potentially self powered, by batteries, which are charged, again, via USB. A switch turns it on, and 16 bit sound comes out a standard stereo 3.5mm jack. Like a laptop; it is "handtop". Four bars on top feel your fingers and two woven antennae below sense flesh, complimented by a battery of buttons. There are red lights.

Analog Emulation

The process of porting diagrams becomes very interesting and you can learn a lot when emulating analogs.  What does this mean?  Well, basically I mean to refer to writing digital code that tries to act the same way as an analog synth.  But there is also the poetry of the meaning of these two words: analog used to refer to that synthesizers were modeling physical processes such as cannonballs, missiles, and other war departments; emulation refers more to a sort of imitation, even mockery.  Let's not let our digital code make a mockery of analog!  One example I can bring forth, is that triangle wave oscillators are usually constructed in computer music, with phase accumulators and wave tables.  This makes a decent simulacrum of the mechanism, and it is preferred because you can thus control the spectral content with band-limiting.  But it is still a simulacrum.  Why not actually build the oscillators like sampled bouncy balls, and thus maintain control of bounce and bounds?  Thus, all the oscillators in the shnth actually have a variable for the ball, which is incremented or decremented, decided by a boolean, that represents the hysteresis loop.  Thus there can be "horse oscillators" with upper bounds and lower bounds as inputs, for rolling up fourses patches.  

the bouncing ball (sports) analogy

Allowing control of bounce and bounds, the analog concepts, yields an important artifact of digitalization: that the two taken together allow rational control of pitch.  Rational refers to Just Intonation, a tuning system pioneered by the ancients but fully described in a modern context by Harry Partch.  It simply means, describing pitch relationships using ratios of numerator and denominator.  I call these snippets of code "nume/deno oscillators," because the speed of bounce is numerator, and the width of bounds is denominator; they are complimentary.  Furthermore, they allow grey intermediary values to be described, without using floating point, or fixed point arithmetic.  In fact, the Shnth uses only an Arm Cortex-M3, which is only integer math.  The decision to use this chipset was made after I wrote the program "Justints," which graphically represents triangle wave tuning systems, using a synthesis core of only integer math, and successfully deployed it on mac, win and lin.  In exploring triangle waves and just intonation with the Shnth, two modalities of tuning movement revealed themselves: kingal and queenal.  Kingal is taking the nume and deno separately and moving them; queenal moves through the compound space melismatically, by having a perspexCUBE, precompiled linked list of all ratio possibilities, in order of actual pitch.  Justints was written in an "8bit pitch space" so they highest prime is 243 or thereabouts.  That yields about 64k unique ratios, so the queenal movement can be very microtonal indeed.  But furthermore, Justints allows you to control the prime-limit of the tuning, so queenal can become a sort of pythagorean pentatonic with a prime limit of 3. 

As I spoke of earlier, the Shnth is an attempt to do classic computer music in an embedded setting.  Granular synthesis was a big goal, but we could only fit a limited number in.  Thus it is the sound, the hallmark of granular synthesis, but unlimited clouds are not possible.  I like it better, with limitations, and I think you will too!  It was an adventure, quite frustrating at times, especially programming the USB stack.  But everything folds over, and the USB code may have even informed the more creative, sonic codes.  Here's two pdfs for the benefit of the audience:

Computer Music Coloring Book

Friendship Bracelets: Deconstructing Triangle Waves